Primera Condición de Equilibrio

Carlos Julián

En este artículo hablaremos sobre la primera condición de equilibrio o también conocida como equilibrio traslacional, se dice que un cuerpo se encuentra en equilibrio si:

a) El cuerpo se encuentra en reposo con respecto a un marco de referencia.

b) El cuerpo se encuentra en movimiento rectilíneo uniforme (Equilibrio traslacional)

Una forma de generalizar la primera condición de equilibrio, es expresarla matemáticamente como la suma vectorial de todas las fuerzas que actúan sobre un cuerpo y que dichas sumas den cero.

Suma de Fuerzas

Esto quiere decir que:

Suma de fuerzas en x

Y también:

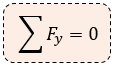
suma de fuerzas en y

📃 Ejercicios Resueltos de la Primera Condición de Equilibrio

Problema 1.- La magnitud de la fuerza F para que el cuerpo que se ilustra se encuentre en equilibrio es:

Equilibrio Traslacional

Solución:

Para poder resolver problemas de equilibrio, siempre es importante contar con un diagrama de cuerpo libre. Entonces decimos que:

equilibrio traslacional

Procedemos a descomponer las fuerzas en sus componentes y se aplica la primera condición de equilibrio.

Comenzando por descomponer la fuerza en "x" = Fx

$\displaystyle {{F}_{x}}=F\cos 30{}^\circ =F\left( \frac{\sqrt{3}}{2} \right)=\frac{\sqrt{3}}{2}F$

Ahora hacemos lo mismo pero para la fuerza en "y" = Fy

$\displaystyle {{F}_{y}}=Fsen30{}^\circ =F\left( \frac{1}{2} \right)=\frac{1}{2}F$

Realizando las suma de las fuerzas en "x"

$\displaystyle \sum{{{F}_{x}}=0\to -{{F}_{x}}+{{F}_{x}}=0}$

Ahora hacemos las sumas de las fuerzas en "y"

$\displaystyle \sum{{{F}_{y}}=0\to {{F}_{y}}+{{F}_{y}}-900N=0}$

$\displaystyle 2{{F}_{y}}-900N=0$

$\displaystyle 2{{F}_{y}}=900N$

Ahora despejando a Fy

$\displaystyle {{F}_{y}}=450N$

Pero como lo que deseamos encontrar es la magnitud de la fuerza, decimos:

$\displaystyle \frac{1}{2}F=450N$

Despejando a "F"

$\displaystyle F=2\left( 450 \right)N=900N$

Respuesta:

La magnitud de la fuerza es de 900 N

Sigue los siguientes temas

Deja una respuesta Cancelar la respuesta

Subir

🤓 Estamos en Whatsapp 👉Únete a nuestro canal